
Fillotassi, questa sconosciuta
- Enrico Costanzo
- 2 Maggio 2013
- Ambiente & Natura
- 0 Comments

C’è una geometria nascosta nella natura. I cristalli seguono regolarità geometriche, formando strutture a volte strabilianti. Tali regolarità non sono esclusive degli oggetti inanimati, ma sono presenti anche negli esseri viventi. Il regno delle piante non fa eccezione e, anzi, è forse qui che le geometrie nascoste diventano più facilmente riconoscibili, almeno per l’occhio attento. Cosa accomuna, ad esempio, una margherita a uno strobilo (o pigna [Fig. 1])? In primo luogo, lo strobilo e il fiore della margherita sono strutture complesse. Lo strobilo è formato da strutture legnose più piccole (brattee), dove si trovano i semi. Il cosiddetto “fiore” della margherita è in realtà composto da numerosi fiori (in senso botanico). I “petali” bianchi sono infatti singoli fiori, così come i cilindri gialli al centro del capolino (fiori tubulosi). Guardando attentamente, salta all’occhio come le brattee dello strobilo e i fiori tubulosi seguano in realtà la medesima geometria: una spirale. Questa disposizione la si ritrova in numerose piante, ed in particolare nel meristema apicale, da cui vengono originati gli organi fogliari. Proprio la disposizione delle foglie prende il nome di fillotassi (dal greco phyllon – foglia, e taxis – disposizione). Anche la pianta più studiata dai biologi vegetali, l’Arabidopsis thaliana (Fig. 2), presenta una fillotassi a spirale.

La fillotassi a spirale non è l’unica. Ne esistono numerose altre (le foglie possono trovarsi su di un solo lato dello stelo – fillotassi monostica -, oppure le foglie sono disposte su due lati opposti – fillotassi distica -, ecc.). Tuttavia, i motivi a spirale hanno da sempre affascinato l’uomo, e la fillotassi spiralata è quindi stata tra le prime ad attirare l’attenzione di filosofi naturali e … matematici. Si scoprì che l’angolo tra due foglie successive è sempre vicino a 137°. Questo non è un numero qualunque. È infatti in relazione con una nota serie numerica, la serie di Fibonacci, dove ogni elemento della serie è dato dalla somma dei due che lo precedono (la serie di Fibonacci è del tipo: 0, 1, 1, 2, 3, 5, 8, … . 2 è infatti dato da 1 + 1, 3 da 2 + 1, 5 da 3 + 2, ecc.). Nel tentativo di descrivere al meglio la fillotassi spiralata, e di decifrarne il mistero, è stato perfino scoperto un “Teorema Fondamentale della Fillotassi” (1). Nonostante questi progressi, la domanda di base “come fa una pianta a produrre foglie sempre con un angolo di 137°?” non aveva ancora trovato una risposta soddisfacente. Alcuni fisici decisero di raccogliere la sfida. Negli anni ’90, i fisici Douady e Couder realizzarono un ingegnoso esperimento: gocce di materiale ferromagnetico venivano fatte cadere dall’alto su di un piatto contenente un olio speciale, in modo che, una volta cadute, le gocce potessero spostarsi lungo il piatto praticamente senza attrito. Il tutto era immerso in un campo magnetico verticale, in grado di agire sulle gocce di materiale ferromagnetico (Fig. 3, ridisegnato da [2]). In questo apparato c’erano due aspetti essenziali: le gocce magnetizzate tendono a respingersi tra loro, e il campo magnetico non è omogeneo. Il campo è minimo al centro del piatto e massimo in periferia, così che le gocce cadute al centro tendono a spostarsi verso il bordo esterno del piatto, ma mano che altre ne cadono. Come si può osservare dal video originale dell’esperimento (http://www.math.smith.edu/phyllo/Assets/Movies/DouadyCouderExp5.9MB.mov), le gocce vanno a disporsi nel piatto esattamente come farebbero i primordi fogliari di un meristema apicale!
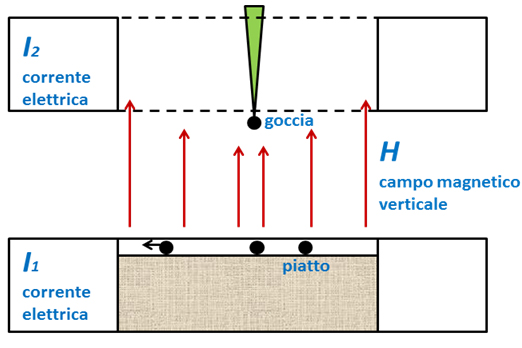
Naturalmente, nella realtà, né i primordi delle foglie sono costituiti da materiale ferromagnetico, né i meristemi vegetali sono immersi in un campo magnetico. Se l’analogia tra un apparato fisico ed un meristema vegetale funziona davvero, allora deve esserci sotto qualcosa di meno evidente e di più profondo ad accomunare i due sistemi. Un merito notevole, però, l’esperimento di Douady e Couder lo aveva: mostrava chiaramente come anche le geometrie tipiche degli esseri viventi non fossero un’esclusiva di questi ultimi, suggerendo inoltre che le leggi della fisica non possono essere del tutto ignorate quando si cominciano a studiare i fenomeni legati alla forma.
Occorre dire però che già da tempo (già verso gli anni ’50), i biologi vegetali avevano cominciato a studiare quelle che possono essere definite le “regole del gioco” di un meristema apicale. Una teoria, in particolare, aveva riscosso particolare successo: la teoria dei campi inibitori.
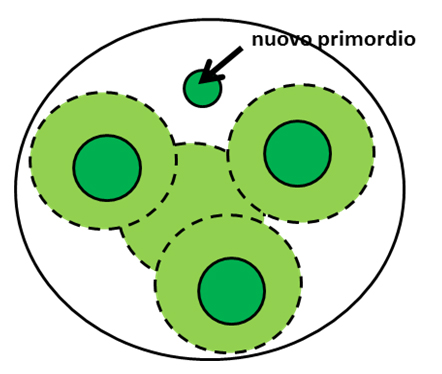
In pratica, secondo questa teoria, un primordio fogliare crea attorno a sé un campo (per esempio, potrebbe farlo grazie alla produzione di uno specifico segnale) in grado d’impedire la creazione di un nuovo primordio. Di conseguenza, un nuovo primordio può formarsi soltanto nel punto lasciato libero dai campi generati dai diversi primordi (Fig. 4). Seguendo queste regole del gioco, un po’ come se il meristema fosse una scacchiera ed i primordi le pedine, è possibile ottenere una fillotassi spiralata. Questo è molto interessante. Si tratta infatti delle stesse “regole del gioco” seguite anche dalle gocce magnetizzate nell’esperimento di Douady e Couder. Ma, se qui era in gioco un campo magnetico, cosa poteva essere all’origine del campo inibitore nella pianta?
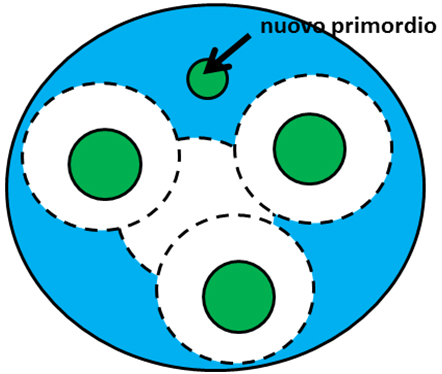
È noto che le piante dispongono di diverse sostanze chimiche in grado di trasportare un segnale, i cosiddetti ormoni. Si trovò che un ormone in particolare era associato con la formazione dei primordi. Questo ormone, da tempo noto ai fisiologi vegetali, è l’auxina. Lo studio dell’auxina può esser fatto risalire allo stesso Darwin, anche se la sua struttura chimica venne svelata soltanto all’inizio degli anni ’30. Oggi sappiamo che l’auxina svolge un ruolo chiave nelle piante, essendo coinvolta in numerosi processi di crescita e sviluppo, da sola o assieme ad altri ormoni. Tra questi processi c’è anche l’origine dei primordi che determina, in definitiva, la fillotassi. Si scoprì che la concentrazione dell’ormone auxina presenta un massimo in corrispondenza dei primordi, mentre la concentrazione scende drasticamente nella zona tutta intorno al primordio. Sembra quindi che la teoria del campo inibitore sia valida, ma rovesciata! Più che dalla presenza d’un inibitore (Fig. 4), il campo è dato dall’assenza dell’attivatore (Fig. 5), cioè l’auxina.
Ma come spiegare la distribuzione dell’auxina? L’auxina si muove da cellula a cellula, così che nei tessuti vegetali sono presenti dei veri e propri flussi di auxina. In alcuni punti si accumula, in altri scorre via, proprio come il corso di un fiume. Le cellule delle piante dispongono di veri e propri canali per l’auxina. Si tratta di proteine particolari che consentono all’auxina di entrare nella cellula, oppure di uscirne. Le proteine che consentono all’auxina di uscire (chiamate PIN), sono distribuite polarmente (cioè, sono disposte su di un solo lato della cellula). Se quindi immaginiamo di mettere in fila diverse cellule orientate nel modo giusto, l’auxina sarà costretta a seguire un flusso preciso. Ecco quindi che i picchi di auxina nei primordi, e i campi inibitori dovuti alla bassa concentrazione di auxina attorno ad essi, si possono interpretare con la diversa orientazione delle proteine PIN nelle varie cellule.
Come si è visto, anche in biologia, partendo da ipotesi astratte e piuttosto astruse (le “regole del gioco” che regolano la fillotassi), si arriva poi ad mettere in luce i meccanismi sottostanti (i “campi inibitori” ed il ruolo dell’auxina). Ma il mistero della fillotassi non è stato ancora svelato del tutto. Ci sono ancora diverse domande che attendono una risposta. Ad esempio: come fanno le proteine PIN a sapere dove orientarsi? L’auxina è davvero l’unico segnale a regolare la fillotassi? O ce ne sono anche altri? E le forze fisiche possono giocare un ruolo anche nel meristema (così come facevano nell’esperimento di Douady e Coyder)? E se sì, quale? La ricerca prosegue…
Costanzo Enrico
2 maggio 2013
Riferimenti:
1 – Adler, I.; Barabe, D.; Jean, R.V. A history of the study of phyllotaxis. In Annals of Botany, 80:231-244 (1997).
2 – Douady, S.; Couder, Y. Phyllotaxis as a dynamical self-organizing process . In Journal of Theoretical Biology, 178:255-274 (1996).
Per approfondire:
Traas J. Phyllotaxis. In Development, 140:249-253 (2013).




